


Solar Station Construction Plans by Ben Peterson -- ebook
will be released to subscribers in:
soon!



 1
1




 2
2




 5
5





 1
1




 6
6




I never fail. I don't believe in it. I only succeed at finding what doesn't work.
 1
1




 1
1




Brenda
Bloom where you are planted.
http://restfultrailsfoodforestgarden.blogspot.com/
 2
2




 3
3




www.thehappypermaculturalist.wordpress.com
 4
4




 3
3




 5
5




oracle wrote:
If you consume brewers yeast on a regular basis, like a tablespoon or so a day it will lessen the amount mosquitos are attracted to you.

Idle dreamer
 2
2




The ultimate goal of farming is not the growing of crops, but the cultivation and perfection of human beings. - Masanobu Fukuoka
 2
2




 3
3





Idle dreamer
 6
6




 5
5




 7
7




The dragonfly nymph eats mosquitoes at all stages of development and is quite effective in controlling populations. Although bats and Purple Martins can be prodigious consumers of insects, many of which are pests, less than 1% of their diet typically consists of mosquitoes. Neither bats nor Purple Martins are known to control or even significantly reduce mosquito populations.
 4
4




 Methinks you can tell I got fishing on the brain when I wrote thins. I was watching a couple bass feed in the edges of the pond. Somehow Bats in the previous post translated to bass
Methinks you can tell I got fishing on the brain when I wrote thins. I was watching a couple bass feed in the edges of the pond. Somehow Bats in the previous post translated to bass 
 1
1




 4
4




 3
3




How permies.com works
What is a Mother Tree ?
 1
1













dolmen wrote:
reading this it suddenly hit me ... do they favour one blood group over another? I've been out with friends and they were left alone and there was clouds of the critters on me!
I've tried the garlic and almost everything else I've ever heard off without any success.
One time my face became so swollen with bites my eyes were closed I need to keep away from them, as they won't keep away from me!
Cheers
I never fail. I don't believe in it. I only succeed at finding what doesn't work.




Sometimes the answer is not to cross an old bridge, nor to burn it, but to build a better bridge.

 1
1




 4
4




 3
3










 9
9




solarguy2003 wrote:
I have some bats, but no bat houses yet. Do you have plans for yours?
That would be excellent.
troy
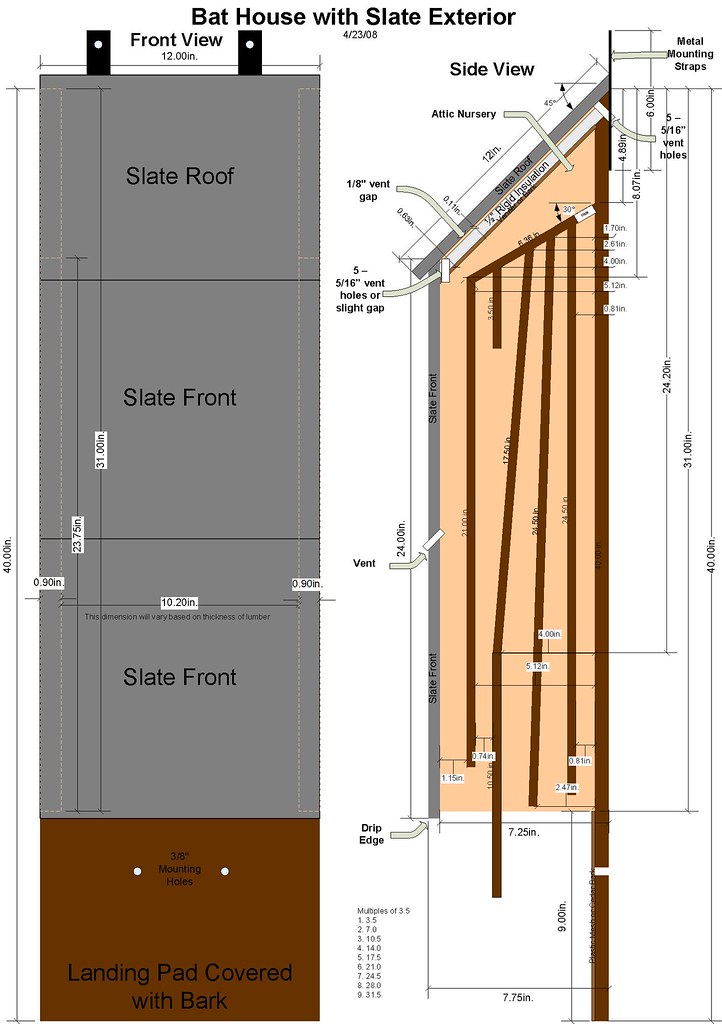



 2
2










 2
2




 1
1




John Polk wrote:
Those bat houses look too close to the ground. Bats have predators too.
Ten to 12 feet above ground will attract more bats.
I never fail. I don't believe in it. I only succeed at finding what doesn't work.
 3
3







 2
2










 2
2




John Polk wrote:
Nice looking houses. Does the slate help them with their echo location?
 1
1





|
Doe, a deer, a female deer. Ray, a pocketful of sun. Me, a name, I call my tiny ad ...
Learn Permaculture through a little hard work
https://wheaton-labs.com/bootcamp
|






